| Step of Proof: fincr_wf |
12,41 |
|
Inference at * 1 4
Iof proof for Lemma fincr wf:
.....eq aux..... NILNIL
1. i : 
2. f : {f | i:{z: | z (
| z ( i,j. i < j) i}
i,j. i < j) i} 
 if (i =
if (i =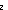 0) then
0) then  else {f(i - 1)...} fi }
else {f(i - 1)...} fi }
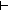 if (i =
if (i =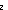 0) then
0) then  else {f(i - 1)...} fi
else {f(i - 1)...} fi  Type
Type
 by ((AbReduce (-1))
by ((AbReduce (-1))
 CollapseTHEN (Assert
CollapseTHEN (Assert  j:{k:
j:{k: | k < i} . f(j)
| k < i} . f(j) 
 ))
))
 C1: .....assertion..... NILNIL
C1: .....assertion..... NILNIL
 C1: 2. f : {f | i:{z:
C1: 2. f : {f | i:{z: | z < i}
| z < i} 
 if (i =
if (i =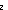 0) then
0) then  else {f(i - 1)...} fi }
else {f(i - 1)...} fi }
 C1:
C1: 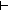
 j:{k:
j:{k: | k < i} . f(j)
| k < i} . f(j) 

 C2:
C2:
 C2: 2. f : {f | i:{z:
C2: 2. f : {f | i:{z: | z < i}
| z < i} 
 if (i =
if (i =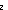 0) then
0) then  else {f(i - 1)...} fi }
else {f(i - 1)...} fi }
 C2: 3.
C2: 3.  j:{k:
j:{k: | k < i} . f(j)
| k < i} . f(j) 

 C2:
C2: 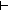 if (i =
if (i =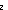 0) then
0) then  else {f(i - 1)...} fi
else {f(i - 1)...} fi  Type
Type
 C.
C.